We work on a range of different topics, currently mainly focusing on mechanisms and properties of unconventional and topological superconductors. We use a wide range of theoretical techniques, from analytically tractable Green’s function methods to large-scale numerical calculations of inhomogeneous superconducting systems and strongly correlated materials, also including complementary ab-initio calculations. Below are short descriptions of our current main activities.
Using Nanoscale Inhomogeneity to Enhance Superconductivity
Superconductivity is a uniquely quantum mechanical phenomenon that despite decades of intense research is still very hard to control. It is heavily dependent on the density of states (DOS) around zero energy, but this DOS tunability has so far remained largely untapped. This activity aims to theoretically create and enhance superconductivity by producing large DOS peaks at zero energy using nanoscale inhomogeneity. A rare, not yet understood, example is twisted bilayer graphene, an all-carbon material not assumed to be superconducting. Here small twist angles produce an inhomogeneous moiré structure hosting large zero-energy DOS peaks that have recently been shown to create superconductivity. Within this activity we aim to understand, as well as enhance, superconductivity in moiré structures in both graphene and topological insulators. Importantly, we also work on finding other new and distinct mechanisms of nanoscale inhomogeneity and zero-energy DOS peaks enhancing superconductivity, such as disorder or quasicrystal structures. We also study how zero-energy DOS peaks may create a superconducting phase crystal in different superconductors, generalizing findings from high-temperature cuprate superconductor surfaces, see figure. Due to its nanoscale phase modulations and spontaneous supercurrents, the phase crystal dramatically enriches the superconducting properties. Taken together, this project aims to create an entirely new, inhomogeneous, landscape for superconductivity.
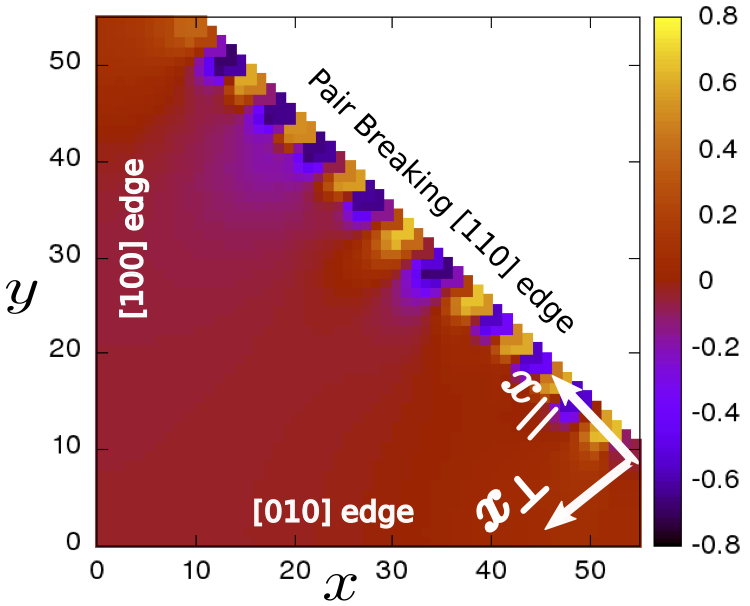
Superconducting phase crystal at the [110] cuprate high-temperature superconductor surface visualized by plotting in color scale the phase sin(theta) of the d-wave order parameter. Later dimensions are given in terms of the lattice constant. Adapted from Chakraborty, Löfwander, Fogelström, and Black-Schaffer, npj Quantum Mater. 7, 44 (2022)
New Frontiers for Topological States of Matter
This activity aims to theoretically discover and characterize entirely new quantum states of matter by novel combinations of global topology and local superconducting order. The discovery of a vast amount of different topological states of matter has completely revolutionized physics the last ten years. The defining property of topological matter is the global non-trivial topology of the electronic structure. This is fundamentally different from the traditional way of classifying matter, where local order parameters instead are the key concept, such as the magnetization in a magnet. In topological superconductors these two disparate views of matter naturally merge, as they have both a global non-trivial topology and a local (superconducting) order.
Topological superconductors are a newly discovered class of materials with features uniquely advantageous for quantum computing. They have lately generated an immense amount of attention due to the possibility of them having effective Majorana fermions at surfaces, vortices, and other defects. Approximately one can say that a Majorana fermion is half an electron, or more accurately, in a system with Majorana fermions the wave function of an electron has split up into two separate parts, see figure below. This non-local property of two Majorana fermions can be used for exceptionally fault-tolerant quantum computing. A quantum computer uses the quantum nature of matter to represent data and perform calculations and can be exponentially faster than any classical supercomputer. However, quantum systems are generally extremely sensitive to disturbances and we are still far from being able to construct useful quantum computers. Topological superconductors with Majorana fermions avoid this extreme sensitivity by using the non-local nature of the Majorana fermions, which automatically make them very robust.
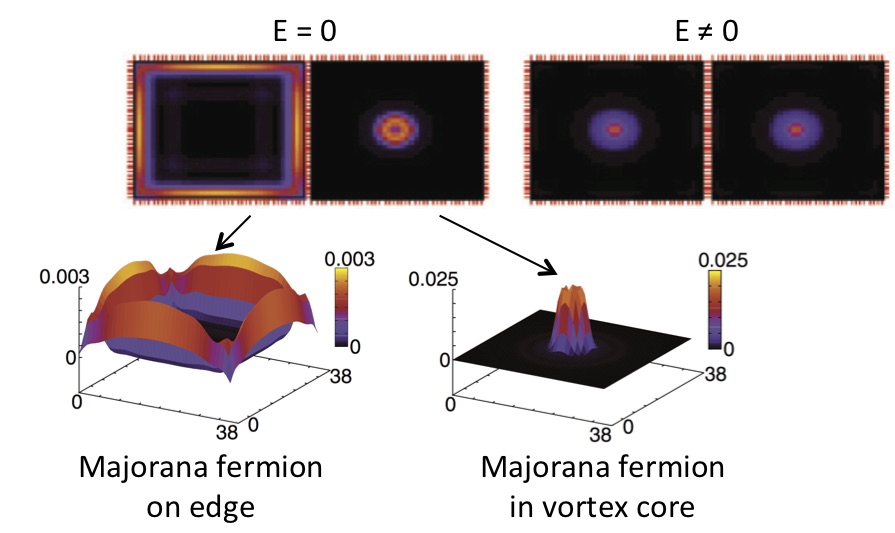
Single electronic state at zero energy divided up into two spatially separated Majorana fermions: one at the edge of the sample and one in a superconducting vortex core. States at non-zero energy are not spatially split and form regular electronic levels. Adapted from Björnson and Black-Schaffer, Phys. Rev. B 88, 024501 (2013).
We are pursuing several systematic approaches to find new topological superconductors, using different but interlinked concepts. These range from focusing on using complex but still common normal-state electronic structures, such as flat energy dispersions and multiorbital configurations, to exploring how time-reversal symmetry can be spontaneously broken in known superconductors and thus generate non-trivial topology. We are also using nanostructuring to achieve both novel phases and sculpture artificial boundaries in topological matter.
New Mechanisms and Materials for Odd-Frequency Superconductivity
Odd-frequency superconductivity is a unique superconducting state that is odd in time or, equivalently, frequency, which is opposite to the ordinary behavior of superconductivity.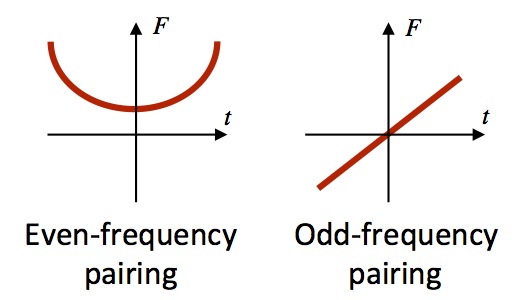 
It has been realized to be the absolute key to understand the surprising physics of superconductor-ferromagnet (SF) structures and has also enabled the whole emerging field of superconducting spintronics. Within this activity we aim to discover and explore entirely new mechanisms and materials for odd-frequency superconductivity, to both generate a much deeper understanding of superconductivity and open for entirely new functionalities. Importantly, we generalize and apply our initial discoveries of two new odd-frequency mechanisms, present in bulk multiband superconductors and in hybrid structures between topological insulators and conventional superconductors, respectively. In both cases odd-frequency superconductivity is generated without any need for ferromagnets or interfaces, completely different from the situation in SF structures.
The goal in this activity is to significantly expand the concept and importance of odd-frequency superconductivity to a very wide class of materials, ranging from multiband, bilayer, and nanoscale superconductors to topological and Weyl superconductors. One example is the chiral and multiband superconductor Sr2RuO4 as illustrated in the figure below. We also aim to establish the connection between topology and odd-frequency pairing, which needs to be addressed in order to understand topological superconductors, as well as incorporate new materials and functionality into traditional SF structures.
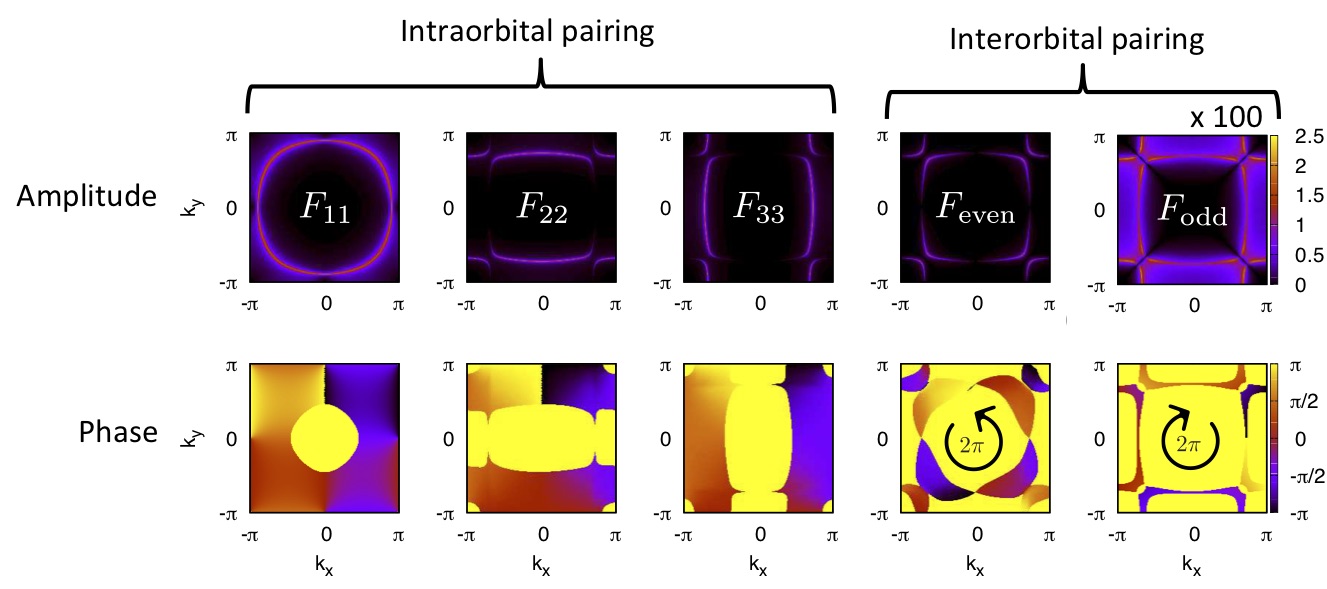
Chiral p+ip superconductivity in Sr2RuO4 divided into intraorbital contributions within the three low-energy orbitals and even- and odd-frequency interorbital pairing. Adapted from Komendova and Black-Schaffer, Phys. Rev. Lett. 119, 087001 (2017).
Dynamic Quantum Matter
Quantum dynamics as a material design principle is an emerging paradigm in condensed matter physics. The answers to basic questions about the nature of the orders, dynamics, coherence, and dissipation of dynamic quantum matter are still unknown. Within this activity, we aim at addressing some of the most basic questions about dynamic quantum matter: the nature of the orders in the time domain of quantum mechanics, the emergence of entangled orders, and the role of dissipation on quantum orders.
Our goal is to predict, engineer, and probe non-equilibrium phases that have no equilibrium analogue. To accomplish these goals, we investigate external drivers that stabilize existing states by enhancing their robustness against noise and ultimately also investigate the non-equilibrium states that do not have analogues in equilibrium, as well as study energy dissipation and localization, including through non-Hermitian effects, that play fundamental roles in limiting and enabling non-equilibrium states. Through a collaborative effort we aim at developing new theoretical models and methods able to understand and accurately predict the creation and control of novel dynamical quantum states of matter. Our theoretical efforts are supplemented by key experimental measurements using ultrafast, coherent photon probes with energies from the meV (terahertz) to the keV (x-rays) range.
This activity is a joint theory-experiment project together with the research groups of Alexander Balatsky (Nordita), Jens Bardarson (KTH), Emil Bergholtz and Stefano Bonetti (Stockholm).