Ultracold atoms

Quantum simulating lattice models with ultracold atoms. Ultracold atoms are loaded into a periodic potential created e.g. by stationary light waves generated via laser (top). Moving in the lattice' lowest Bloch band, these atoms realize Hubbard-type models near-perfectly. Model parameters such as tunneling amplitude J and on-site interaction U are set by the properties of the atoms, the periodic potential and e.g. external magnetic fields (bottom). All these can be subject of very precise experimental control.
Since the first Bose Einstein condensates (BECs) of neutral atoms were achieved in 1995, the ongoing research into using such many-body quantum states of matter as a quantum simulator has tremendously expanded the scope of research on strongly correlated quantum matter.

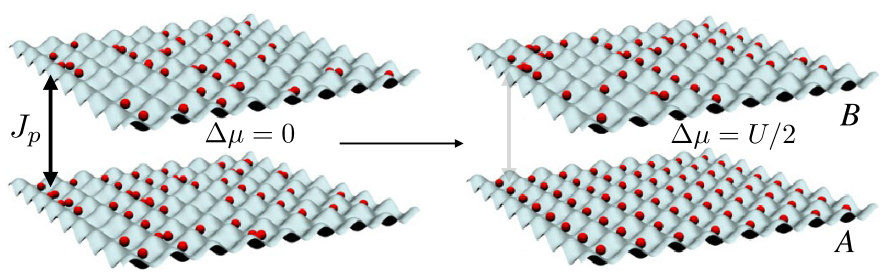
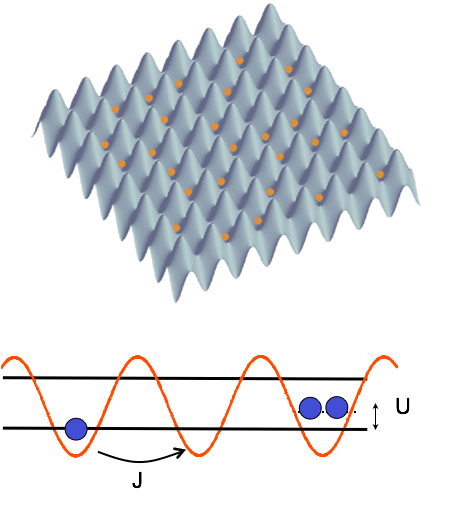
For lattice models of strongly correlated quantum particles, quantum simulation works the following way: confine ultracold bosonic or fermionic atoms inside the lowest Bloch band(s) of an optical lattice, which is formed by (a) standing laser wave(s).

As such systems can realize many of the important and difficult-to-solve models of condensed matter physics, like e.g. the 2D Hubbard model doped away from unit filling, the equilibrium state of this system could reveal the models ground state - thus ''quantum simulation'': solving a model for which theory cannot yet compute the ground state reliably, via precise and controlled experimental realization of the model at low entropy/temperature.

My work in the domain of quantum simulation is concerned with three key topics:

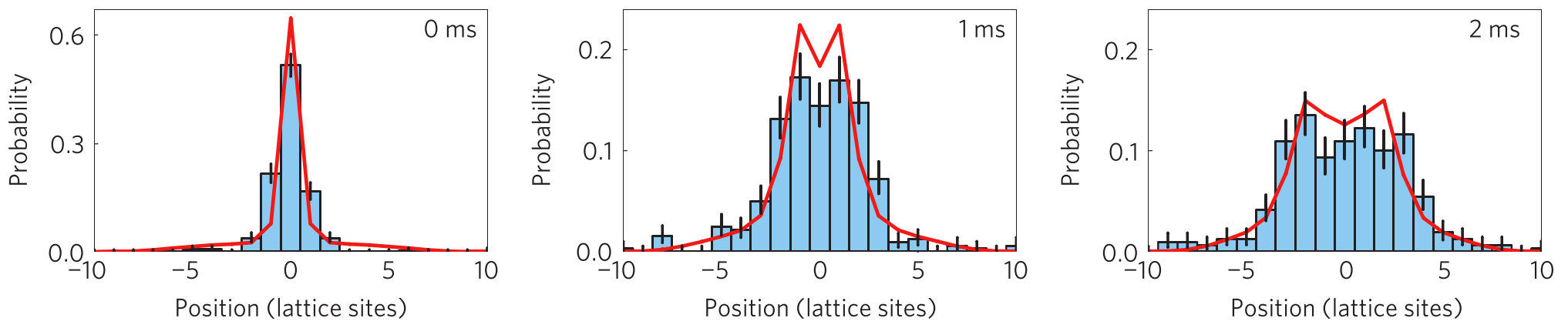
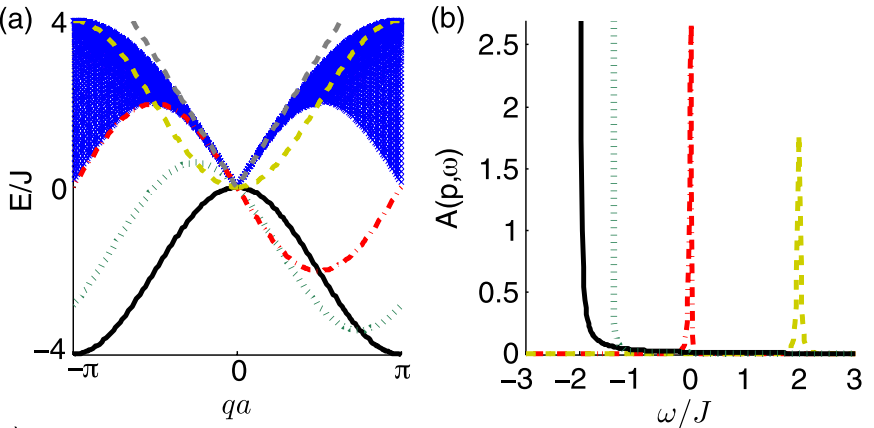
(1) Static and dynamic phenomena in quantum matter, such as disordered systems, dissipatively driven phases and mobile quantum impurities in 1D.

(2) Obtaining lattice-confined atoms at low entropies for quantum simulation.

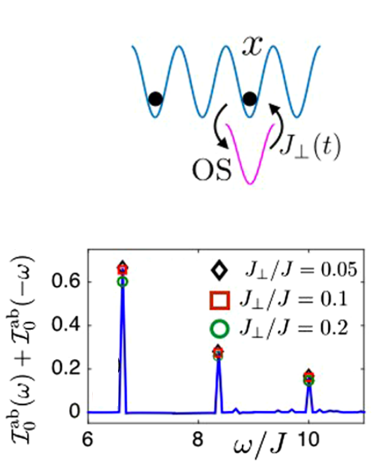
(3) Measuring the properties of the realized state inside the lattice.

New insight and new physics from correlated ultracold atoms: disordered systems, dissipatively driven phases and mobile quantum impurities


(back to top)

My earliest published work was concerned with showing the capabilities of interacting atoms moving inside purposefully disordered optical lattices to quantum-simulate hard-to-solve problems in quantum percolation and spin glass theory [Phys. Rev. Lett 93 40401 (2004), Phys. Rev. A 72 63616 (2005), J. Phys. B - Atom. Mol. Opt. Phys. 39, 121 (2006), Acta. Phys. Pol. A 109, 89 (2006)].

Later revisiting this topic showed how the creation of two physically identical replicas of the same disordered system and measuring their cross-system overlap would allow to probe for the Bose glass phase, one of the basic models in the study of disordered quantum many-body systems [New J. Phys. 10, 073032 (2008)].

My first direct involvement in using the potential of lattice-confined ultracold atoms to create completely new many-body states of quantum matter came in the theory-experiment collaboration with the group of J. Hecker-Denschlag (Innsbruck) on metastable repulsively bound pairs [Nature 441, 853 (2006)]. This work was the start of an ongoing line of my work in modelling and thus understanding many-body experiments through strong DMRG numerics.

I was further involved in an influential collaborative project to design dissipatively driven many-body phases of correlated atoms, such as a lattice BEC of bosons or η-paired states of superfluid fermion pairs. [Nat. Phys. 4, 878 (2008)]. This scheme is based on engineering couplings of the lattice confined atoms to many disconnected local dissipative reservoirs.

It could then be shown under which conditions many such local actions drive the system collectively towards a well-defined global state [Phys. Rev. A 78, 42307 (2008)].

Afterwards, mobile quantum impurities inside a 1D quantum liquid became a major focus of my work.

I could show that any impurity newly injected into the system belongs to a new dynamical universality class, in which the impurity loses all quasiparticle properties and is characterized by subdiffusive motion, i.e. logarithmically slow motion, slower than any power law, instead [Phys. Rev. Lett. 113, 70601 (2014); c.f. figure].

Flanking this work was a collaboration on the full non-equilibrium dynamics of a 'kicked' impurity oscillating inside a parabolically confined 1D quantum liquid [New J. Phys. 15, 045018 (2013)].

These theoretical works were complemented by research as lead theorist on two high-impact collaborations with experimental groups.

With the group of F. Minardi at LENS (Firenze) we studied the polaronic mass shift of an impurity oscillating inside a 1D mass and its dependence on the bath-impurity interaction [Phys. Rev. A 85 23623 (2012)].

And with the group of I. Bloch at MPQ Garching (München) we provided an unprecedented look at the quantum-coherent propagation of both spin waves and polarons, resolved in time and space [Nat. Phys. 9, 235 (2013); c.f. figure].

(back to top)
Quantum coherent propagation of a polaron, resolved in time and space. From Nat. Phys. 9, 235 (2013). Shown is the evolution of an impurity released at t=0 at different points in time inside a 1D lattice-superfluid. Blue bars denote experimental measurements, red lines DMRG simulations. Based on their agreement, this establishes this experiment as providing quantitative access to the polaronic mass shift.
Universal subdiffusive dynamics of impurity injected into 1D quantum liquid at low momenta. From Phys. Rev. Lett. 113, 70601 (2014). Subfigure (a) shows the nonzero support for excitations of 1D free fermions at half filling in the space of momentum and frequency, i.e. energy (blue area). Superimposed are energy curves for the impurity emitting a phonon of momentum q inside those 1D fermions, for different initial impurity momenta. At low initial momenta, these curves have no intersection with the excitation spectrum at nonzero q (black and green curves) - only virtual phonons can be emitted. Subfigure (b) shows that this corresponds to the subdiffusive universality class, where the impurity's spectral function A(p,ω) is not quasi-particle like at all, but shows power-law threshold behaviour θ(ω-εp)/(ω-εp)Δ(p) instead (εp: impurity dispersion), which corresponds to sudiffusive motion in real space and time. The DMRG numerics in Phys. Rev. Lett. 113, 70601 (2014) is combined with analytical arguments to show that this is universally true for any 1D quantum liquid.
In-lattice cooling of atoms through disentangling. From Phys. Rev. Lett. 120, 60401 (2018), which shows the condition under which the disentangling of two layers of a bilayer system may result in cooling. As sketched here, slowly ramping up a chemical potential difference between the two layers, for e.g. a Bose-Hubbard Hamiltonian, and afterwards slowly ramping down interlayer tunneling will result in shifting much of the systems entropy into the top layer, thus effectively cooling the lower layer. In the example shown here, this would result in a Mott insulating state at very low temperatures. This state would then be an excellent starting state for e.g. adiabatic state preparation (see main text). When implemented in a multi-state/multi-species, this would result in magnetically ordered state at very low entropy. The key requirement for disentangling to map into cooling is that all single-particle excitations must be gapped towards the end of the parameter ramp.
Essential to quantum simulation: low-entropy states

(back to top)

Even though lattice-confined ultracold atoms excel at precisely mimicking those Hubbard-type models to be quantum simulated, they struggle against one drawback: as the near-total isolation of the atoms from the environment is indispensable for bringing them to ultracold temperatures, it is a challenge to remove any entropy that remains within the atomic cloud once it has been loaded into the optical lattice - there just is no reservoir left into which to shift the excess entropy.

This is a major hurdle for quantum simulation of e.g. the main candidate model to explain high-Tc superconductivity, the doped 2D Hubbard model, as entropies in current experiments are still too high.

To solve this problem, and provide methods to future experiments for producing very-low entropy states for quantum simulation, my research has focussed on both adiabatic state preparation, as well as shifting much of the remaining entropy into a subsystem, thus sacrificing part of the whole in order to bring the remainder to an even lower temperature.

Adiabatic state preparation exploits the available high degree of control over the optical lattice to load the atoms initially into a 'trivial' product state, with e.g. one atom in every second site of a superlattice. Removing the optical superlattice adiabatically would then see this state cross over smoothly into the exact non-trivial ground state of the Hamiltonian of which the ground state is sought.

In my work I have described how this approach can be used to create metastable exact eigenstates with exotic superfluid η-pairing of fermionic atoms as a highly sensitive benchmark state for validating state preparation in a quantum simulator [Phys. Rev. Lett. 104, 240406 (2010).; with A. J. Daley and P. Zoller].

Previously, I had shown that adiabatic state preparation could be used to form the optical lattice analogue of a metastable ground state of bilayer excitons [New J. Phys. 9, 407 (2007); with A. J. Daley, P. Törmä and P. Zoller], as well as the metastable colour superfluid of three-species fermions with strongly extended lifetime due to a many-body Quantum Zeno effect [Phys. Rev. Lett. 103, 240401 (2009); with M. Dalmonte, S. Diehl, W. Hofstetter, P. Zoller and A. J. Daley].

Further work with M. Dolfi and M. Troyer quantified the degree of heating the atoms incur when being loaded into the lattice in the standard manner, and provided prescriptions as to how this heating might be minimized through time-dependent adjustment of the global parabolic trap [Phys. Rev. A 91, 33407 (2015)]

For the other approach, entropy shifting, I have shown together with S. Langer and A. J. Daley, when and how disentangling the two layers of a bilayer system from each other maps to cooling one of the layers. Besides the fundamental interest in such a mapping, we show that this scheme offers a high practical performance, due to the contact between cooled system and entropy sink being equal in size to the subsystem volume, making all entropy transport effectively local [Phys. Rev. Lett. 120, 60401 (2018); c.f. figure].

(back to top)
Measuring observables
(back to top)

The concept of quantum simulation requires measuring the properties of any state prepared in the lattice - i.e. to ''read out'' the result.

With the field of quantum simulation increasingly being advanced by experiments using confocal microscope-based optical lattice setups, which offer unprecedented single-site resolution and manipulation of atoms, previous measuring schemes that offer frequency/time and spatial/momentum resolution are reaching their limits, due to the generally low number of atoms in these setups.

I was part of a wider collaboration to show how the newly available single-site resolution provides a way out of this dilemma, being the basis of a novel in-lattice approach for measuring practically any time- and space-dependent spin-spin correlation function of any effective spin-Hamiltonian that can be realized in such experiments [Phys. Rev. Lett. 111, 147205 (2013)].

I further proposed and theoretically validated a much more general scheme of lattice-assisted spectroscopy applicable to practically any Hamiltonian that could provide frequency-resolved local particle- and hole-spectra [Phys. Rev. Lett. 115, 165301 (2015); c.f. figure]. This scheme can then be generalized further to provide momentum-resolved and higher-order spectral functions.

(back to top)
Measuring local spectral functions for arbitrary lattice models. From Phys. Rev. Lett. 115, 165301 (2015). Confocal-microscope experiments offer single-site detection and manipulation of lattice-confined ultracold atoms. As sketched (top graph), this can be exploited to measure any on-site spectral function for arbitrary lattice models, by applying an oscillating tunneling term selectively from the desired lattice-site to an outcoupling site OS. Using DMRG numerics to validate this approach for different interacting systems (black, red and green markings in lower graph), this work shows that even for non-perturbatively large strengths of outcoupling, the resulting distortion to the exact spectral function (blue line) is weak.