The density matrix renormalization group (DMRG) is a very powerful approach to simulate 1D interacting
quantum systems, in many cases offering quasi-exact precision. As sketched in Figure 1,
it is based on a truncated
Hilbert space: the coefficients needed to represent a many-body-wavefunction
(or density matrix) in a naive product basis, which would be growing exponentially with system size,
are each represented by a series of three-dimensional tensors, with one
tensor for each site of the physical lattice.
The number of parameters contained in all tensors
is much less than the number of coefficients in the 'naive' product basis for most 1D problems
- this is the source of the power of DMRG in 1D. Uniquely for DMRG, this even holds true
within a certain window of time when simulating the evolution of a many-body 1D system that is being perturbed.
The size of the time window here varies very substantially with the strength of the perturbation, whether it is local or system-wide, etc.
The tensors of DMRG remain small for 1D states at or near equilibrium because bipartite quantum entanglement
in 1D usually does not scale with the size of the subsystems. When applying DMRG to 2D lattices,
this is generally no longer true. There, subsystem entanglement SAB grows with the width of the 2D lattice.
To maintain a given accuracy, the tensors of DMRG will therefore have to grow strongly, possibly exponentially.
As a 2D-lattice implies many long-range terms in the DMRG-Hamiltonian, the strong growth of the tensor-sizes further
implies that this Hamiltonian can require a large amount of computer RAM, easily reaching into the TB.
Both these challenges are encapsulated in Figure 2.
However, DMRG remains an extremely interesting method to apply to systems of interacting electrons in 2D lattices.
This is because for such models, which include some of the most important to understand unconventional and high-Tc
superconducting materials - the 2D Hubbard
model, the 2D U-V model, and others - there are no easy options. All methods face great challenges in this domain -
but on critical issues those of DMRG are less severe than others. In particular, it does not suffer from the sign
problem of Quantum Monte Carlo (QMC), and is not biased towards any order as variational QMC can be. Most importantly,
the size of the error in any DMRG-calculation is known, making it possible to extrapolate many observables to zero
approximation error.
Parallel DMRG is build to exploit the capabilities of modern parallel supercomputers with fast
interconnects between the nodes, like the Cray XC-30 and XC-40 machines. It has already seen extensive use in my research,
with a single calculation spread out to up to hundreds of nodes of the
Piz Daint and
Beskow supercomputers. At the same time, pDMRG
can just as well be run on any number of cores of a single node (an earlier,
published,
single-node version forms the re-developed DMRG-module of the
ALPS-library).
That version of the code has been used more widely already, such as
here,
here,
and here.
The multiple layers of inbuilt parallelism in pDMRG (see next point) make it capable of dealing both with the large tensors and many
long-range terms in the DMRG-Hamiltonian that appear when studying e.g. 2D lattices of repulsive
fermions, and that also feature heavily in this groups research on engineering unconventional
superconductivity from systems of 1D electrons.
To enable DMRG to apply many nodes of a distributed-memory parallel supercomputer to a single calculation,
pDMRG was designed using the Message Passing Interface (MPI), a standard for distributed computing. The code
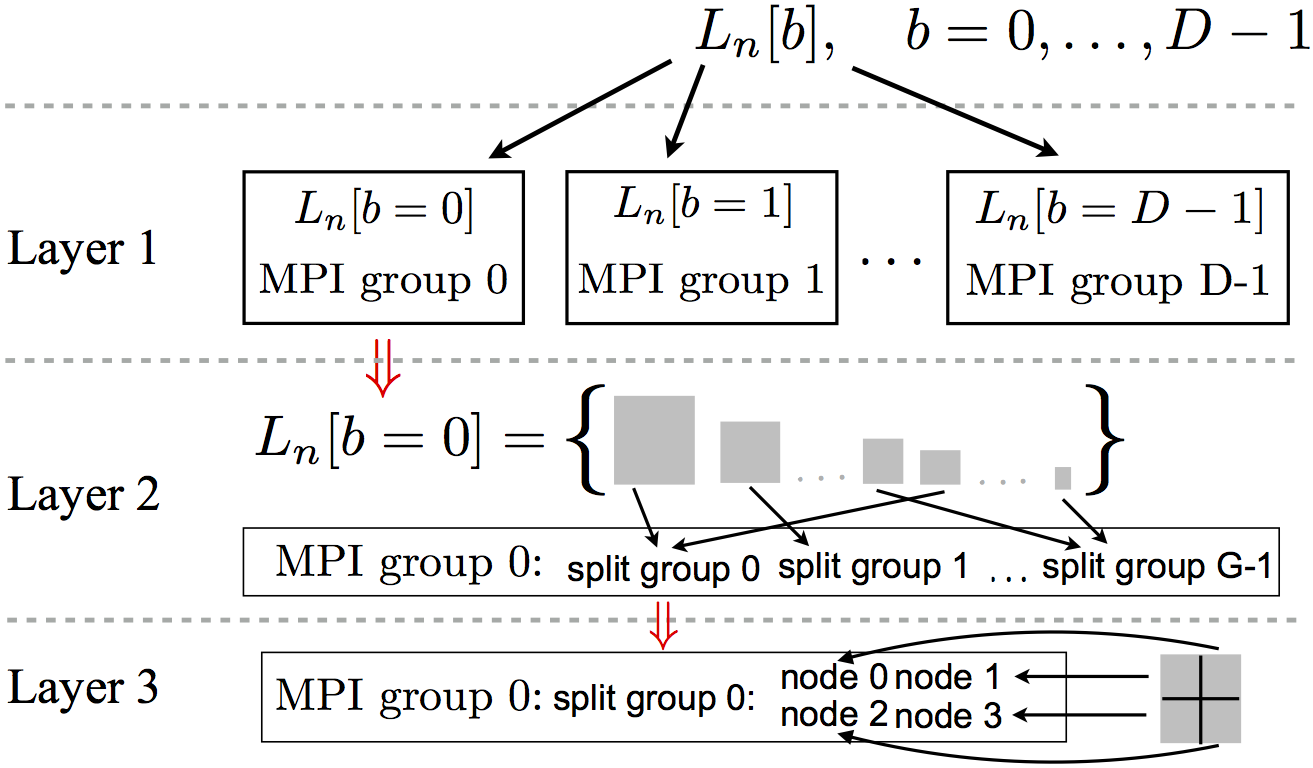
offers three layers of parallelism, as summarized in Figure 3, where an example is illustrated using the left boundary
of a DMRG problem (left and right boundaries encode the Hamiltonian in the left/right subsystem, represented
in the optimal eigenstates DMRG had previously determined for these subsystems):
- Layer 1 exploits that the boundaries, usually the largest objects of a DMRG-calculation, are vectors of block-sparse matrices
of length D. It distributes the D elements of both these vectors, each element being a block-sparse matrix,
in a size-ordered, round-robin fashion within the global group of MPI-groups. Each of the MPI-groups within this group may
encompass several nodes of the compute cluster.
- Layer 2 then allows to distribute the dense matrices comprising each boundary element among
MPI-subgroups (into which each main group can be split).
- Layer 3 allows to distribute tiles of a dense matrix to different compute nodes held by each of the split-off subgroups
(as dense matrices can themselves become large, they are always stored in tiled format).
In the Jacobi-Davidson eigensolver of pDMRG, the tensor contractions become dot-products of vectors of matrices.
For this, MPI groups communicate via MPI_Allreduce. When shifting to
the next pair of sites, the number of boundaries can change, which results in a redistribution of elements among
the MPI-processes, using asynchronous point-to-point transfers. On each node, operations are executed in two steps.
A dry-run collects all linear algebra operations (mostly GEMM and
AXPY). In the second step the directed acyclic operation-graph is executed
in parallel on several threads. This abstract approach optimizes performance, autonomously exploiting hidden
operational parallelism. The basic linear algebra operations are then explicitly unrolled between tiles of the dense
matrix and dispatched to the underlying BLAS library.
Developing pDMRG was one central goal of the MAQUIS collaboration, running from 2010 to 2013,
between the groups of Thierry Giamarchi (lead PI, University of Geneva), Frederic Mila (EPF Lausanne) and Matthias Troyer (ETH Zürich).
With funding by the Swiss government under its HP2C initiative, and supported
by the Swiss National Supercomputing Centre (CSCS), the objective of MAQUIS was to have physicists work closely together
with project-embedded IT specialists to deliver codes for quantum many-body numerics capable of exploiting next-generation
distributed-memory parallel supercomputers, of which pDMRG is one of the major end results. The scientists and IT specialists
contributing to pDMRG so far have been Bela Bauer, Michele Dolfi, Timothée Ewart, Adrian Kantian, Sebastian Keller,
Alexandr Kosenkov and Matthias Troyer.