Systems in 1D and 2D are central to many intensely-studied phases of correlated electrons.
Among them are unconventionally superconducting (USC) materials resulting from repulsion-mediated pairing of electrons,
as well as exciton condensates based on pairing of electrons and holes. These macroscopic
quantum states are of great fundamental as well as technological interest, as they offer lossless transport
of current and/or energy.
In USC materials, the superconducting phase is generally in direct competition with Mott-insulating and magnetically ordered phases. It presents a great challenge to understand this competition and the physics taking place inside the USC phase, as for example in the ongoing effort to comprehend the mechanism behind high-Tc superconductivity.
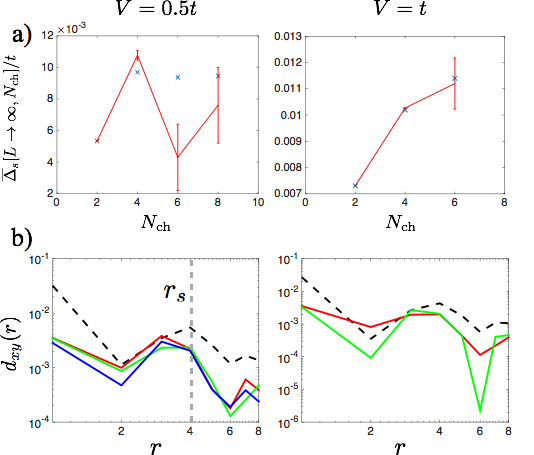
I am working on a paradigmatic case in this domain, the minimal U-V Hubbard model of the organic Bechgaard and Fabre salts. In these materials, repulsively interacting electrons prefer to move along 1D chains (formed by stacks of cationic organic molecules). Weak interchain tunneling of electrons then is found to provide the critical ingredient to tune the system from magnetically ordered insulator to unconventional superconductor. The strong spatial inhomogeneity of this quasi-1D setup provides a critical technical advantage over the weakly doped 2D Hubbard model. This is so because this property allows to use parallel DMRG (pDMRG) to investigate the physics of an USC phase and how electron pairing may arise from purely repulsive interactions with reliable numerics in the limit of infinite system size. The results of large-scale calculations (with single simulations spread over dozens or even hundreds of nodes) on the Piz Daint parallel supercomputer offer strong indirect evidence from reliable numerics that a minimal model of an USC material can enter a superconducting phase at strong coupling, something had proven to be very difficult so far.
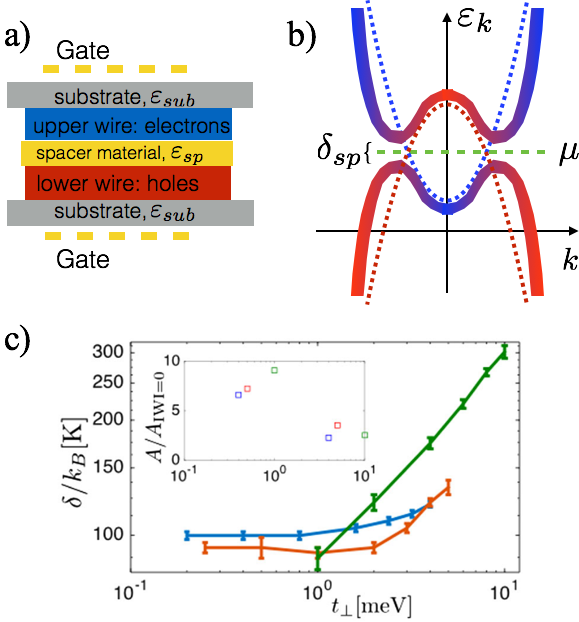
In my research on bilayer excitons, the situation is somewhat reversed. Theory is certain in principle as to how these stable bound states of electrons and holes form and then may enter a condensate phase. However, outside the Quantum Hall regime (low temperature, high magnetic field) so far no experiment on 2D bilayers could show a condensate forming. While there is no canonical explanation for this yet, important factors are known to be the impact of screening on the electron-hole attraction that is critical for exciton formation, and the problem of having to achieve nesting of two 2D Fermi surfaces experimentally. My focus here is how 1D bilayer systems remove the problem of screening, and provide a chance to observe exciton condensates at temperatures of up to a few hundred Kelvin.
(back to top)
In USC materials, the superconducting phase is generally in direct competition with Mott-insulating and magnetically ordered phases. It presents a great challenge to understand this competition and the physics taking place inside the USC phase, as for example in the ongoing effort to comprehend the mechanism behind high-Tc superconductivity.
I am working on a paradigmatic case in this domain, the minimal U-V Hubbard model of the organic Bechgaard and Fabre salts. In these materials, repulsively interacting electrons prefer to move along 1D chains (formed by stacks of cationic organic molecules). Weak interchain tunneling of electrons then is found to provide the critical ingredient to tune the system from magnetically ordered insulator to unconventional superconductor. The strong spatial inhomogeneity of this quasi-1D setup provides a critical technical advantage over the weakly doped 2D Hubbard model. This is so because this property allows to use parallel DMRG (pDMRG) to investigate the physics of an USC phase and how electron pairing may arise from purely repulsive interactions with reliable numerics in the limit of infinite system size. The results of large-scale calculations (with single simulations spread over dozens or even hundreds of nodes) on the Piz Daint parallel supercomputer offer strong indirect evidence from reliable numerics that a minimal model of an USC material can enter a superconducting phase at strong coupling, something had proven to be very difficult so far.
In my research on bilayer excitons, the situation is somewhat reversed. Theory is certain in principle as to how these stable bound states of electrons and holes form and then may enter a condensate phase. However, outside the Quantum Hall regime (low temperature, high magnetic field) so far no experiment on 2D bilayers could show a condensate forming. While there is no canonical explanation for this yet, important factors are known to be the impact of screening on the electron-hole attraction that is critical for exciton formation, and the problem of having to achieve nesting of two 2D Fermi surfaces experimentally. My focus here is how 1D bilayer systems remove the problem of screening, and provide a chance to observe exciton condensates at temperatures of up to a few hundred Kelvin.
(back to top)